1) Determinar a área do triângulo a seguir considerando que a sua base mede 23 metros e a altura 12 metros.


2) Calcule a área do triângulo a seguir:
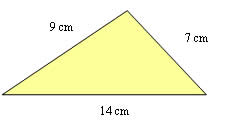
p = (9 + 7 + 14) / 2
p = 30 / 2
p = 15
A = √15(15 – 9)(15 – 7)(15 – 14)
A = √15 * 6 * 8 * 1
A = √720
A = 26,83 cm2(aproximadamente)
3) Um triângulo possui lados medindo 5 cm e 8 cm, respectivamente. Sabendo que ele possui um ângulo na base medindo 30º, determine a área desse triângulo.

4) Calcule a área da região triangular a seguir sabendo que os lados medem: 40, 31 e 52.
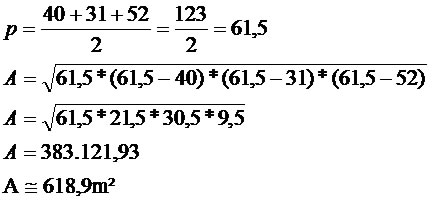
Temos que o triângulo em questão possui área de 618,9 m².
Se o triângulo for equilátero de lado l, sua área A pode ser obtida com:
Ou então usando sua altura h e a fórmula da base vezes a altura. A altura h de um triângulo equilátero é:
Vale notar que essas duas fórmulas para os triângulos equiláteros são obtidas usando as funções seno ou cosseno e usando a altura do triângulo, que o divide ao meio em dois triângulos retângulos iguais.
5) Um triângulo equilátero possui área de 16√3 cm². Determine a medida do lado desse triângulo.
Solução:
Temos que A = 16√3 cm². Logo,
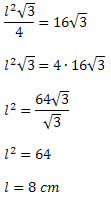
6) Determine a medida da altura de um triângulo equilátero de área 25√3 cm².
Solução:

Podemos determinar a altura do triângulo equilátero se as medidas de seus lados forem conhecidas. Assim, vamos encontrar a medida do lado utilizando a área que foi dada pelo exercício.
PERÍMETRO DE POLÍGONOS
Perímetro de Quadrados e Retângulos:
Perimetro e Área da Circunferência:
Perímetro e Área do Paralelogramo:
Perímetro e Área do Triângulo
- Perimetro = comprimento + largura + comprimento + largura.
- Área = comprimentro x largura.
Perimetro e Área da Circunferência:
- Perimetro = Pi (3,14) x Raio2 (raio ao quadrado).
- Área = Pi x 2 x Raio2.
Perímetro e Área do Paralelogramo:
- Perímetro = Lado + Lado + Lado +Lado.
- Área = Base x Altura.
Perímetro e Área do Triângulo
- Perímetro = (Base x Altura) / 2 (a dividir por 2).
- Área = Lado x Lado x Lado.
Questões sobre perímetro de figuras planas
1) Se o perímetro de um quadrado é de 64 cm, qual é a medida de cada lado desse quadrado?
Solução:
Sabemos que o quadrado é um quadrilátero com todos os lados congruentes (com a mesma medida). Dessa forma, para determinar a medida de cada lado teremos que dividir o perímetro por 4.
Assim,
L = 64 ÷ 4 = 16 cm
Assim,
L = 64 ÷ 4 = 16 cm
2) Um fazendeiro pretende cercar um terreno retangular de 120 m de comprimento por 90 m de largura. Sabe-se que a cerca terá 5 fios de arame. Quantos metros de arame serão necessários para fazer a cerca? Se o metro de arame custa R$ 15,00, qual será o valor total gasto pelo fazendeiro?

Solução:
Imagine que a cerca terá somente um fio de arame. O total de arame gasto para contornar todo o terreno será igual à medida do perímetro da figura. Como a cerca terá 5 fios de arame, o total gasto será 5 vezes o valor do perímetro.
Cálculo do perímetro:
2p = 120m + 90m + 120m + 90m = 420 m
Total de arame gasto:
5*420 = 2100 m de arame para fazer a cerca.
Como cada metro de arame custa R$ 15,00, o gasto total com a cerca será de:
2100*15 = R$ 31. 500,00
Solução:
Imagine que a cerca terá somente um fio de arame. O total de arame gasto para contornar todo o terreno será igual à medida do perímetro da figura. Como a cerca terá 5 fios de arame, o total gasto será 5 vezes o valor do perímetro.
Cálculo do perímetro:
2p = 120m + 90m + 120m + 90m = 420 m
Total de arame gasto:
5*420 = 2100 m de arame para fazer a cerca.
Como cada metro de arame custa R$ 15,00, o gasto total com a cerca será de:
2100*15 = R$ 31. 500,00
3) Calcular a área de um triângulo retângulo conhecendo o seu perímetro 2p e a altura h relativa à hipotenusa.
Resolução:
Sendo o triângulo retângulo de hipotenusa "a", catetos "b" e "c" e altura relativa à hipotenusa "h". Se sabemos seu perímetro:
a + b + c = 2p
Elevando tudo ao quadrado:
a + b + c = 2p
a2 + b2 + c2 + 2ab + 2bc + 2ac = 4p2
Pelo teorema de Pitágoras b2 + c2 = a2, então:
a2 + b2 + c2 + 2ab + 2bc + 2ac = 4p2
a2 + a2 + 2ab + 2bc + 2ac = 4p2
Chamando a área do triângulo de A, que é a base vezes a altura sobre 2:
ah/2 = A
a = 2A/h
Ou então a área pode ser o produto dos catetos sobre 2:
bc/2 = A
bc = 2A
Então podemos continuar usando isso:
a2 + a2 + 2ab + 2bc + 2ac = 4p2
2a2 + 2ab + 2bc + 2ac = 4p2
2a2 + 2ab + 4A + 2ac = 4p2
2a2 + 2a.(b + c) + 4A = 4p2
E aqui vamos achar que como a + b + c = 2p:
a + b + c = 2p
b + c = 2p - a
Colocando isso também na equação e no lugar de "a" colocando sempre 2A/h:
2a2 + 2a.(b + c) + 4A = 4p2
2a2 + 2a.(2p - a) + 4A = 4p2
2(2A/h)2 + 2(2A/h).(2p - 2A/h) + 4A = 4p2
4) As diagonais de um losango medem 10cm e 24cm. Determine o perímetro do losango.?
Solução:
Se é um losango as duas diagonais se cruzam no ponto médio de cada uma, dai basta achar a hipotenusa do triangulo formado pela metade desses segmentos
x² = 5² + 12²
x² = 25 + 144
x² = 169
x = raiz(169)
x = 13
logo cada lado do losango vale 13
então o perímetro é igual a:
P =13 x 4 = 52 cm
x² = 5² + 12²
x² = 25 + 144
x² = 169
x = raiz(169)
x = 13
logo cada lado do losango vale 13
então o perímetro é igual a:
P =13 x 4 = 52 cm
5) Calcule o perímetro da figura abaixo:
Solução:
2p = 7 cm + 2 cm + 2 cm + 2 cm + 3 cm + 2 cm + 3 cm + 5 cm = 26 cm
FONTE:QUESTÕES DE VESTIBULAR NA NET

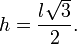
Nenhum comentário:
Postar um comentário